第9章 简单线性回归分析
1. 回归概述
回归与相关
在第8章中,我们学习了相关分析,用于研究两个变量之间联系的紧密程度。
而回归分析则是进一步研究变量间的数量依存关系。
-
相关分析 (Correlation):
- 目的:定性分析。描述两变量间呈直线关系的密切程度和方向。
- 条件:要求 \(X\)、\(Y\) 均为随机变量,且服从双变量正态分布。
-
回归分析 (Regression):
-
目的:定量分析。建立数学方程 \(Y=f(X)\),用自变量 \(X\) 的值去预测应变量 \(Y\) 的值。
-
条件:
- \(Y\)(应变量/因变量/响应变量):必须服从正态分布。
- \(X\)(自变量):可以不服从正态分布。可以是随机变量,也可以是严格控制的确定性变量(如给药剂量)。
-
分类:
-
按自变量个数:简单回归 (1个X)、多重回归 (多个X)。
-
按关系形态:线性回归、非线性回归。
-
-
本章的直线回归其目标是:研究应变量Y对自变量X的数量依存关系。其特点是: 统计关系,X值和Y值的均数的关系,不同于一般数学上的X 和Y的一一对应的函数关系。
简单线性回归的步骤
(1)要以专业知识为依据,确定研究某两个变量之间回归关系的必要性。避免纯粹“玩弄数字游戏”。
(2)绘制两个变量变化的散点图,根据图中各散点的分布情况判断是否值得作线性回归分析。若各散点在不平行于X轴也不垂直于X轴的一条不太宽的带内随机地分布着,则可以继续进行回归分析,否则,没有必要。
(3)统计描述:建立两个变量的回归方程,即求直线方程的截距和斜率。
(4)统计推断:通过假设检验,确定回归方程的统计学意义。
(5)统计应用:利用已建立的回归模型(方程)计算未测量的数据,即插值计算。
2. 简单线性回归模型的建立
绘制散点图
在进行计算前,必须先绘制散点图。 * 作用:直观判断变量间是否存在线性趋势。如果散点呈现“圆盘状”则不宜做直线回归;如果散点分布在一条不太宽的带内,则适合进行直线回归分析。
线性回归方程
-
总体回归方程: $$ \mu_{Y|X} = \alpha + \beta X $$ 其中 \(\alpha\) 为总体截距,\(\beta\) 为总体斜率(回归系数)。 实际观察值 \(Y_i\) 包含抽样误差 \(\epsilon_i\):\(Y_i = \alpha + \beta X_i + \epsilon_i\)。
-
样本回归方程: $$ \hat{Y} = a + bX $$
- \(\hat{Y}\):在 \(X\) 取某值时,总体均值 \(\mu_{Y|X}\) 的点估计值(预测值)。
- \(a\):样本截距(Constant),\(X=0\) 时回归直线在 \(Y\) 轴的截距。
- \(b\):样本回归系数 (Slope),表示 \(X\) 每增加一个单位,\(Y\) 平均改变 \(b\) 个单位。
例题:参数间的关系
记 \(\rho\) 为总体相关系数,\(r\) 为样本相关系数,\(b\) 为样本回归系数,下列( )正确。
A. \(\rho=0\)时,\(r=0\)
B. \(|r|>0\)时,\(b>0\)
C. \(r>0\)时,\(b<0\)
D. \(r<0\)时,\(b<0\)
E. \(|r|=1\)时,\(b=1\)
正确答案: D
解析: 样本回归系数 \(b\) 与样本相关系数 \(r\) 的符号是一致的。
公式关系为:\(b = r \cdot \frac{S_Y}{S_X}\)。
由于标准差 \(S_Y\) 和 \(S_X\) 均为正数,所以 \(b\) 的正负完全取决于 \(r\)。
即:\(r > 0 \Rightarrow b > 0\)(正相关,斜率为正);\(r < 0 \Rightarrow b < 0\)(负相关,斜率为负)。
最小二乘法估计参数估计\(a,b\)
- 原理:求解系数 \(a\)、\(b\),使得残差平方和 (\(SS_{残差}\)) 最小,即各观测点距直线的纵向距离平方和最小。
-
目标函数: $$ Q = \sum (Y_i - \hat{Y}_i)^2 = \sum (Y_i - (a + bX_i))^2 = min $$ 即保证各实测点 \(Y_i\) 至回归直线的纵向距离的平方和最小。
-
计算公式: $$ b = \frac{\sum(X-\bar{X})(Y-\bar{Y})}{\sum(X-\bar{X})^2} $$ $$ a = \bar{Y} - b\bar{X} $$ 注意:回归直线必定经过均值点 \((\bar{X}, \bar{Y})\)。
例题:最小二乘法的含义
用最小二乘法确定直线回归方程的含义是( )。
A. 各观测点距直线的纵向距离相等
B. 各观测点距直线的纵向距离平方和最小
C. 各观测点距直线的垂直距离相等
D. 各观测点距直线的垂直距离平方和最小
E. 各观测点距直线的纵向距离等于零
正确答案: B
解析: 最小二乘法(Least Squares)的核心思想是使“残差”的平方和最小。在回归分析中,残差定义为实际观测值 \(Y\) 与预测值 \(\hat{Y}\) 之间的差(\(Y - \hat{Y}\)),这在几何上表现为点到直线的纵向距离(Vertical distance),而不是垂直距离(Perpendicular distance)。
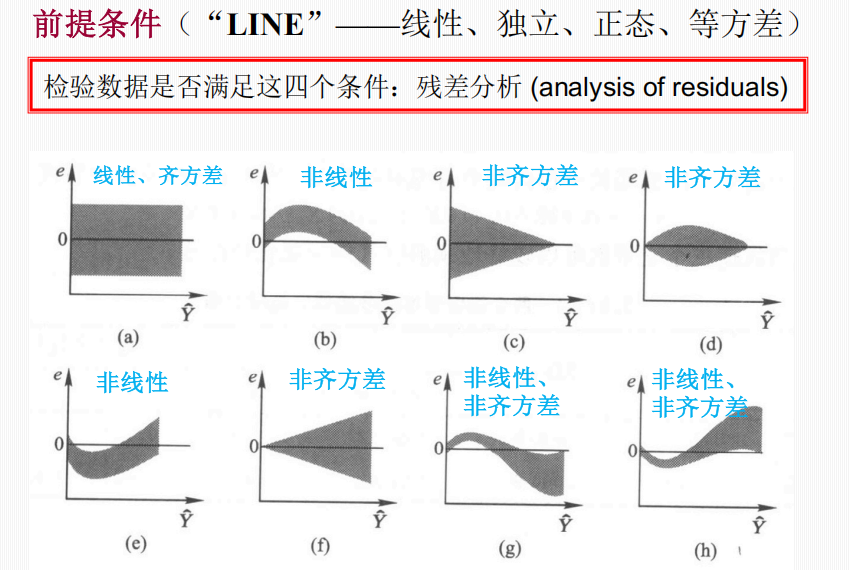
模型的前提条件 (LINE)
应用线性回归模型需满足四个条件,通常通过残差分析来检验:
-
线性 (Linearity):反应变量\(Y\) 的总体均值与自变量 \(X\) 呈线性关系。
-
独立 (Independence):任意两个观察值互相独立。
-
正态 (Normality):在一定范围内任意给定 \(X\),对应的 \(Y\) 服从正态分布。
-
等方差 (Equal Variance / Homoscedasticity):在一定范围内不同 \(X\) 值对应的 \(Y\) 的总体变异程度(方差)相同。
画残差散点图。若残差散点图残差散点随机、均匀地分布在 0 水平线上下,则可定性地满足线性条件;若残差不随预测值的增大而呈现明显的趋势,可以定性地认为满足齐方差条件。
正态性检验要画正态概率图,独立性要做D-W检验。
3. 回归方程的假设检验
建立回归方程后,必须验证这种线性关系是否具有统计学意义(即 \(\beta \neq 0\))。
方差分析 (ANOVA)——回归模型的假设检验
将 \(Y\) 的总变异分解为两部分: $$ \sum(Y-\bar{Y})^2 = \sum(\hat{Y}-\bar{Y})^2 + \sum(Y-\hat{Y})^2 $$ $$ SS_{总} = SS_{回归} + SS_{残差} $$
- \(SS_{总}\):离均差平方和,反映 \(Y\) 的总变异。
- \(SS_{回归}\):回归平方和,由 \(X\) 的变化引起的 \(Y\) 的变异(模型可解释部分)。
- \(SS_{残差}\):残差平方和,随机误差。
检验统计量 \(F\): $$ F = \frac{MS_{回归}}{MS_{残差}} = \frac{SS_{回归}/\nu_{回归}}{SS_{残差}/\nu_{残差}} $$ 其中自由度:\(\nu_{回归}=1\) (简单线性回归),\(\nu_{残差}=n-2\)。
假设:\(H_0: \beta = 0\),自变量对因变量没有贡献。
若 \(P < \alpha\),认为回归模型成立。
例题:相关系数与变异分解 (r=1)
如果直线相关系数 \(r=1\),则一定有( )。
A. \(SS_{总} = SS_{残}\)
B. \(SS_{残} = SS_{回}\)
C. \(SS_{总} = SS_{回}\)
D. \(SS_{总} \ge SS_{回}\)
E. 以上都不正确
正确答案: C
解析: 当 \(r=1\) 时(完全相关),所有观测点完全落在回归直线上,预测值与实际值没有偏差,因此残差平方和 \(SS_{残} = 0\)。
根据总变异分解公式:\(SS_{总} = SS_{回} + SS_{残}\)。
因为 \(SS_{残} = 0\),所以 \(SS_{总} = SS_{回}\)。这说明自变量 \(X\) 解释了因变量 \(Y\) 的全部变异。
例题:逐步回归中的变异变化
逐步回归分析中,若增加自变量的个数,则( )。
A. 回归平方和与残差平方和均增大
B. 回归平方和与残差平方和均减小
C. 总平方和与回归平方和均增大
D. 回归平方和增大,残差平方和减小
E. 总平方和与回归平方和均减小
正确答案: D
解析: 总平方和 (\(SS_{总}\)) 是固定的(取决于因变量 \(Y\) 的数据本身)。
当模型中加入新的自变量时,模型对数据的拟合程度通常会提高(至少不会变差),这意味着模型能解释的变异 (\(SS_{回归}\)) 会增大。
根据公式 \(SS_{总} = SS_{回归} + SS_{残差}\),既然 \(SS_{总}\) 不变且 \(SS_{回归}\) 增大,那么 \(SS_{残差}\) 必然减小。
回归系数\(\beta\)的检验——\(t\) 检验
用于检验总体回归系数 \(\beta\) 是否为 0。
-
假设:\(H_0: \beta = 0\)。
-
统计量:\(t = \frac{b - 0}{S_b}\),其中 \(S_b\) 为回归系数的标准误。
-
对于简单线性回归(只有一个自变量),\(t\) 检验与方差分析 (\(F\) 检验) 是等价的,且 \(t^2 = F\)。
例题:相关系数与回归统计量的关系
如果两样本的相关系数 \(r_1 = r_2\),样本量 \(n_1 = n_2\),那么( )。
A. 回归系数 \(b_1 = b_2\)
B. 回归系数 \(b_1 < b_2\)
C. 回归系数 \(b_1 > b_2\)
D. \(t\) 统计量 \(t_{b1} = t_{r1}\)
E. 以上均错
正确答案: D
解析: 在简单线性回归中,对回归系数 \(\beta=0\) 的检验(\(t\) 检验)与对相关系数 \(\rho=0\) 的检验是等价的。
检验统计量的公式在数值上是相同的:
\(t_b = \frac{b}{S_b}\) 和 \(t_r = \frac{r}{\sqrt{(1-r^2)/(n-2)}}\)。
虽然本题选项D表述略显模糊(可能指第一组的回归t值等于第一组的相关t值,这是对的;或者指两组的t值相等),但在已知 \(r_1=r_2\) 且 \(n_1=n_2\) 的情况下,两组数据的 \(t\) 统计量计算结果必然相等,且对于同一组数据,回归系数的假设检验 \(t\) 值等于相关系数的假设检验 \(t\) 值。
选项 A, B, C 不一定成立,因为 \(b = r \frac{S_Y}{S_X}\),即使 \(r\) 相同,如果两组数据的标准差 \(S_Y, S_X\) 不同,\(b\) 也会不同。
决定系数\(R^2\)
-
定义:\(R^2 = \frac{SS_{回归}}{SS_{总}}\)。
-
意义:反映了自变量 \(X\) 对应变量 \(Y\) 总变异的解释程度(百分比)。
-
取值:\(0 \le R^2 \le 1\)。
-
联系:在简单线性回归中,\(R^2 = r^2\)(相关系数的平方)。
例题:相关系数与变异分解 (r=0)
如果变量 \(X, Y\) 直线相关系数 \(r=0\),正确的是( )。
A. 直线回归的截距等于0
B. 不是线性相关,但可能有多复杂的相依关系
C. 直线回归的 \(SS_{残}\) 等于 \(SS_{总}\)
D. 直线回归的 \(SS_{残} = SS_{回}\)
E. 直线回归的 \(SS_{残}\) 等于0
正确答案: B, C
解析:
B正确:相关系数 \(r=0\) 仅表示两变量间无线性相关关系,并不排除它们之间存在非线性(如曲线)关系。
C正确:当 \(r=0\) 时,决定系数 \(R^2 = r^2 = 0\)。这意味着回归模型无法解释任何变异,即 \(SS_{回} = 0\)。根据公式 \(SS_{总} = SS_{回} + SS_{残}\),可得 \(SS_{残} = SS_{总}\)。
A错误:当 \(r=0\) 时,斜率 \(b=0\),回归方程简化为 \(\hat{Y} = \bar{Y}\)(均值),截距为 \(\bar{Y}\),不一定等于0。
4. 线性回归的应用
预测
利用回归方程 \(\hat{Y} = a + bX\),根据已知的 \(X\) 值推测 \(Y\) 值。包括两种类型的区间估计:
- 总体均数的置信区间 (Confidence Interval for Mean):
- 估计 \(X\) 取某值时,\(Y\) 的总体均值 \(\mu_{Y|X}\) 的范围。
- 公式涉及标准误 \(S_{\hat{Y}}\)。
- 区间较窄。
- 个体值的容许区间/预测区间 (Prediction Interval for Individual):
- 估计 \(X\) 取某值时,某一个体观察值 \(Y\) 的波动范围。
- 公式涉及标准差 \(S_Y\)(包含了残差变异和抽样误差)。
- 区间较宽。
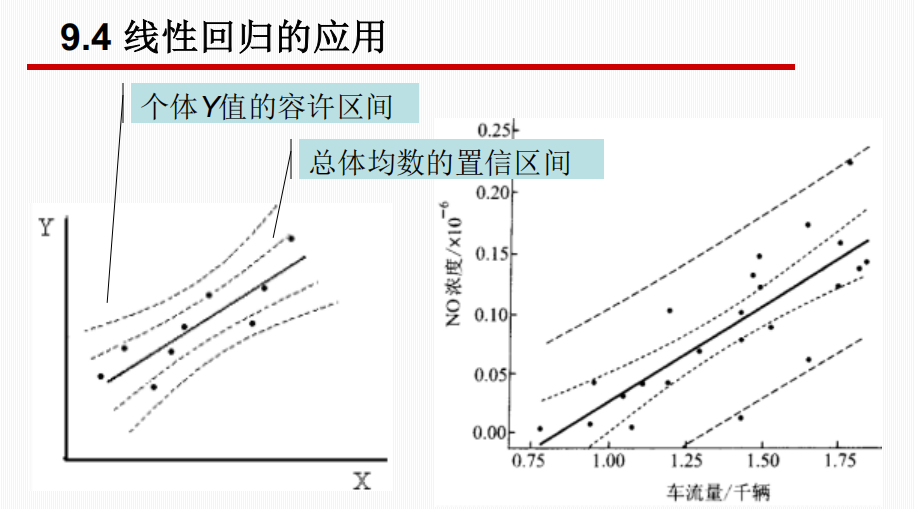
在相同回归线的置信度下,个体值的预测区间比均值的置信区间带更宽。 对于给定的自变量值,这个区间给出了一个新的个体观测值有 95% 的概率会落入的范围。它比置信区间更宽,因为它不仅要考虑总体均值的不确定性,还要考虑个体观测值本身的波动。由于标准误是X的函数,所以在均数位置的置信带宽度最小,越远离该均数点,置信带宽度越大。
如果我们重复进行抽样和回归分析,每次都计算自变量为某个值时的 95% 置信区间,那么大约有 95% 的这些区间会包含真实的总体均值。这个区间有很大的概率(95%)包含这个真实的均值。它反映的是我们对总体参数(均值)估计的不确定性。
控制
如果要将 \(Y\) 控制在某个范围内,可以通过回归方程反推需要将 \(X\) 控制在什么范围。
5. 小结与注意事项
- 步骤:绘图(散点图)\(\rightarrow\) 建摸(求 \(a, b\))\(\rightarrow\) 检验(\(F\) 或 \(t\) 检验, \(R^2\))\(\rightarrow\) 应用(预测)。
- 异常值 (Outliers):异常点对回归影响很大,不应草率删除,需寻找原因。
- 数据合并:来自不同总体(如不同亚群)的数据不能简单合并进行回归,否则可能得出错误的结论(类似辛普森悖论)。
- 外推风险:回归方程通常只在自变量 \(X\) 的观测范围内有效,外推(预测超出范围的 \(X\))可能不准确。