第9章系统稳定性

离散时间系统稳定性

\(h[n]\)为右边序列，\(h[n]=0\)当\(n<0\)时

\(H[z]\)中分母最高次指数\(N\)大于等于分子最高次项指数\(M\)，即传递函数z变换形式极点个数大于等于零点个数

定义：当输入信号收敛时输出信号也收敛，输入有界，输出也有界

判断条件：\(h[n]\)绝对可和，\(h[n]\)傅里叶变换存在，\(h[n]\)的z变换收敛域包含单位圆

z变换中极点在单位圆内部

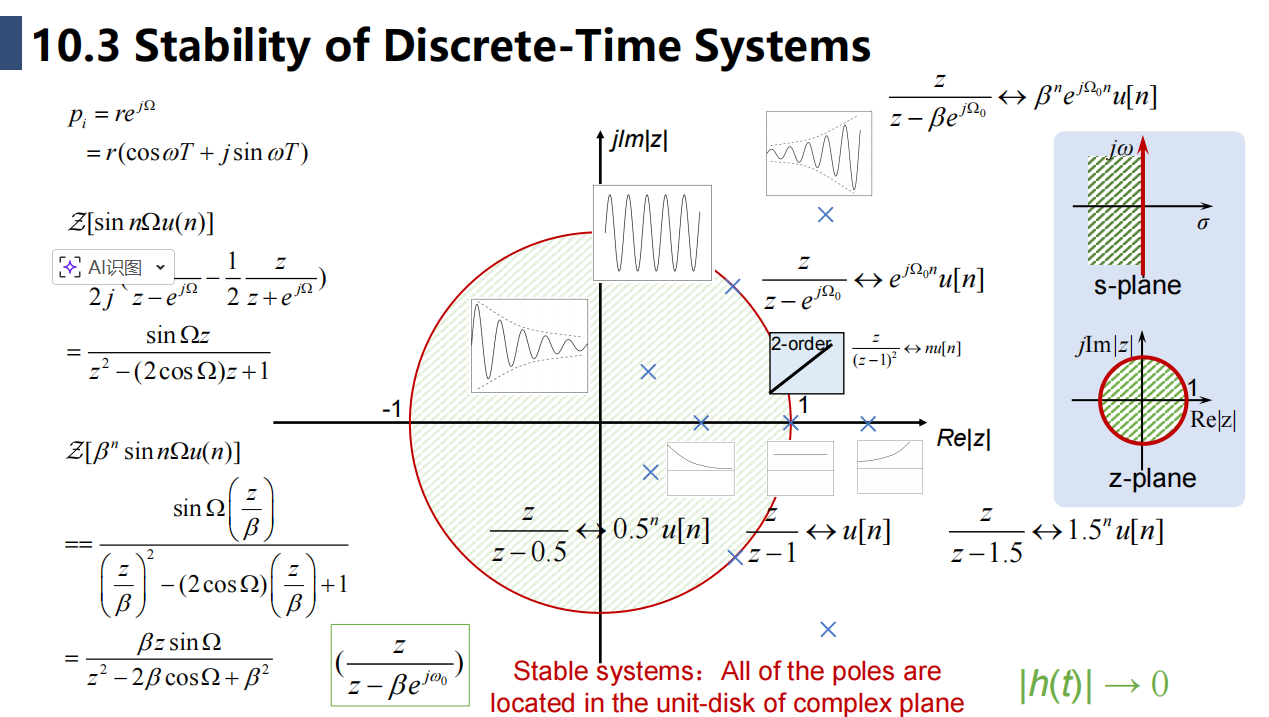
总体描述：收敛域内包含虚轴，注：收敛域内不能有极点

\(h(t)\)绝对可积

\(h(t)\)傅里叶变换存在，拉普拉斯变换收敛域包含虚轴

当\(t<0\)时，\(h(t)=0\)

\(h(t)\)拉氏变换形式中传递函数\(H(s)\)的极点\(p\)的实部小于0，即极点在负半平面（不包含虚轴），收敛域包含虚轴