第6章 离散时间信号和系统的频域分析DTFT和DFT
1.离散时间信号傅里叶变换 DTFT
DTFT的过程
采用采样的思想
\(x(t)\rightarrow x(nT)=x[n]\) $$ X(\omega T)=\sum_{n=-\infty}^{+\infty}x(nT)e^{-j\omega nT} $$ 令\(\omega T=\Omega\), $$ X(\Omega)=\sum_{n=-\infty}^{+\infty}x[n]e^{-j\Omega n} $$ \(\Omega=\frac{\omega}{\omega_s}\cdot 2\pi\),将\(\Omega\)叫作归一化数字角频率,无量纲
DTFT反变换
存在条件
一个有限长序列,它的傅里叶变换一定存在
\(X(\Omega)\)周期性
从采样角度看,由于\(X_s(\omega)\)是\(X(\omega)\)的复制搬移,而\(X(\Omega)\)和\(X_s(\omega)\)相比只是对横坐标做了一个归一化处理,所以必然是周期的,且周期为\(2\pi\)
\(e^{-an}u[n]\)DTFT
若要计算幅值,把\(e^{-j\Omega}\)用欧拉公式展开
常用信号DTFT
单位脉冲序列
单位复指数信号
正弦信号与余弦信号
单位阶跃序列
指数序列
门函数序列
注意时域方波不能直接变成sinc $$ p_{\tau}(\Omega) \leftrightarrow \frac{\tau}{2\pi}\text{sinc}[\frac{\tau n}{2}] $$
DTFT的性质

如何画DTFT
思路:1、因为\(X(Ω)\)是\(2\pi\)为周期的,且Ω 在\(\pi—2\pi\)区域内的|X(Ω)|与\(0—\pi\)区域内的\(|X(Ω)|\)关于\(\pi\)镜像对称,因此只要画出\(0—\pi\)部分的\(|X(Ω)|\)即可
2、可以用一些特殊点定位,比如代入\(\Omega=0, \Omega=\frac{\pi}{4}, \Omega=\frac{\pi}{6}, \Omega=\frac{\pi}{3}, \Omega=\frac{\pi}{2}, \Omega=\pi\),这些点,就可以算出这些频率点对应的幅值\(|X(\Omega)|\),之后将这些点连起来,就可以构成\(|X(\Omega)|\)的大致形状了
DTFT的高频和低频
将任意\(x(t)\)以\(\omega_s\) 的采样角频率采样后,频谱中最高频率理论上为\(\frac{\omega_s}{2}\)
对应的\(\Omega\)值又为π
以\((-\pi,\pi)\)为例,\(|\Omega|\)越接近\(\pi\),为高频;\(|\Omega|\)越接近0,为低频
低通/高通/带通滤波器的判断
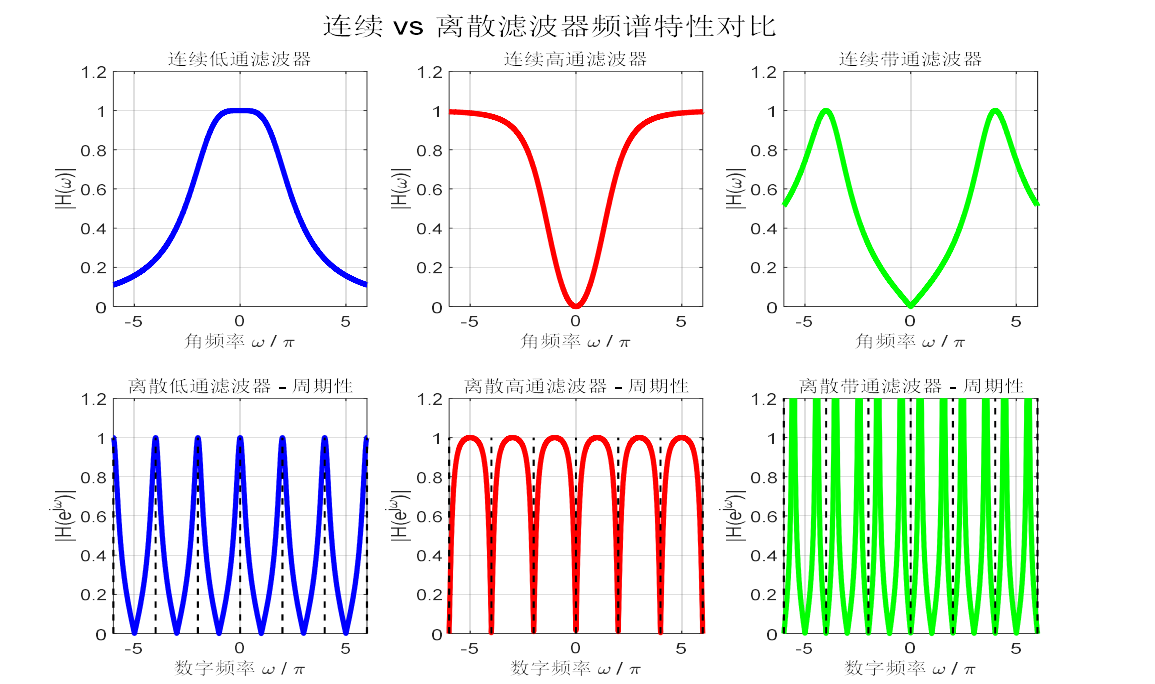
判断DTFT的滤波器,主要看\((-\pi,\pi)\)的区域,若为\((0,2\pi)\),建议将\((\pi,2\pi)\)的段对称到\((-\pi,0)\)
2.离散傅里叶变换 DFT
DFT的过程
DTFT无法在工程上被分析,连续的、无限长的频域也无法被计算机处理,用DFT来离散化DTFT来观测DTFT,即DFT是对DTFT的采样,并取主值周期
前提条件:\(x[n]\)有限长,\(l\le N\),\(N\)和信号长度不一定要相等
将\(\Omega\)离散化,令\(\Omega=\frac{2\pi}{N}k\),\(k\)为频域的离散值 $$ X_k=\sum_{n=0}^{N-1}x[n]e^{\frac{-j2\pi k n}{N}},k=0,1,...,N-1 $$
DFT反变换IDFT
DFT隐藏时域周期化
DFT对DTFT在频率域采样时,会使得\(x[n]\)在时域上进行以\(N\)为周期的周期延拓,因此\(N\ge L\),否则信号会混叠
因此我们对\(X(\Omega)\)取了\(0-2\pi\)的主值周期,即\(X_k\)中\(k=0,1,...,N-1\),所以\(x[n]\)仍然是原信号,或者说是原信号周期延拓后取了主值周期的结果。\(N\)代表一个周期的采样点个数,\(N>L\)时相当于对原信号补零
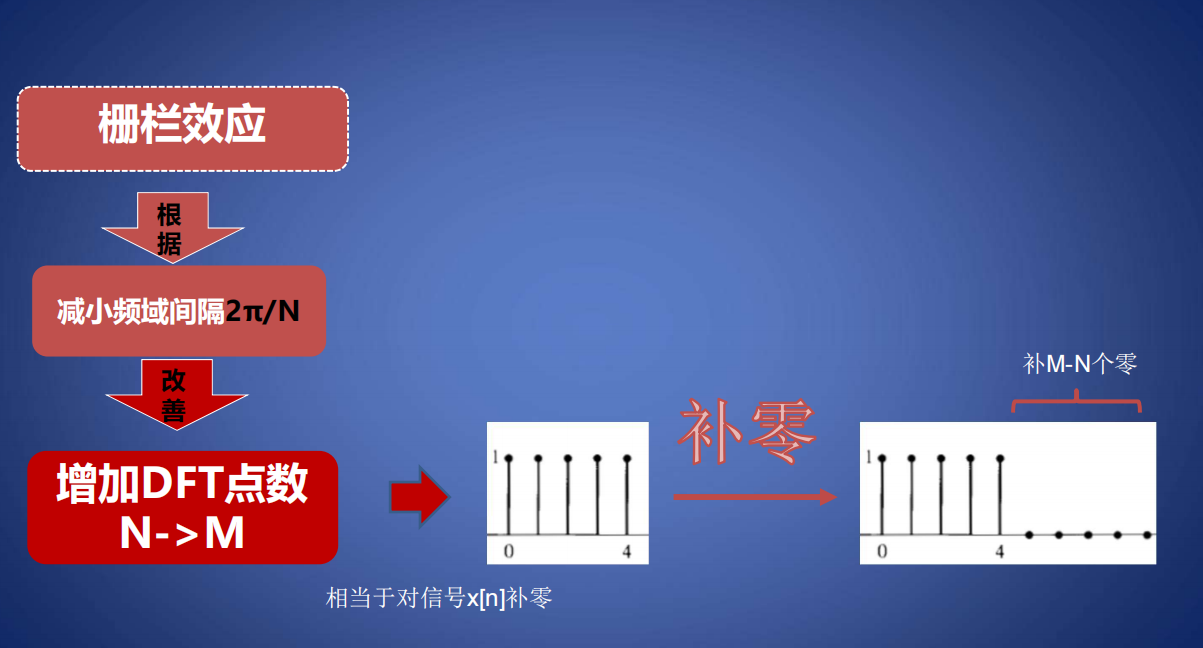
DFT的参数和定义关系


增加记录时间,就能减小\(F_0\),提高频率分辨率
\(X(k)\)的第\(k\)根谱线对应的实际频率\(f_k\)
一道郑婧姐姐复习课提供的真题

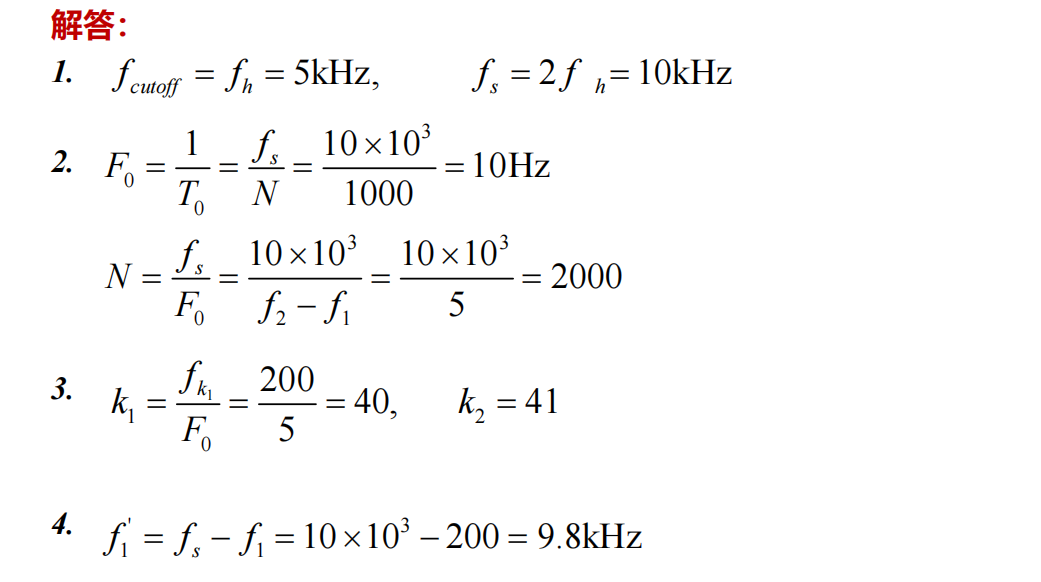
DFT的性质
线性
时移:圆周移位
圆周移位的概念可理解为\(x[n]\)经历周期延拓后再移位最后取主值
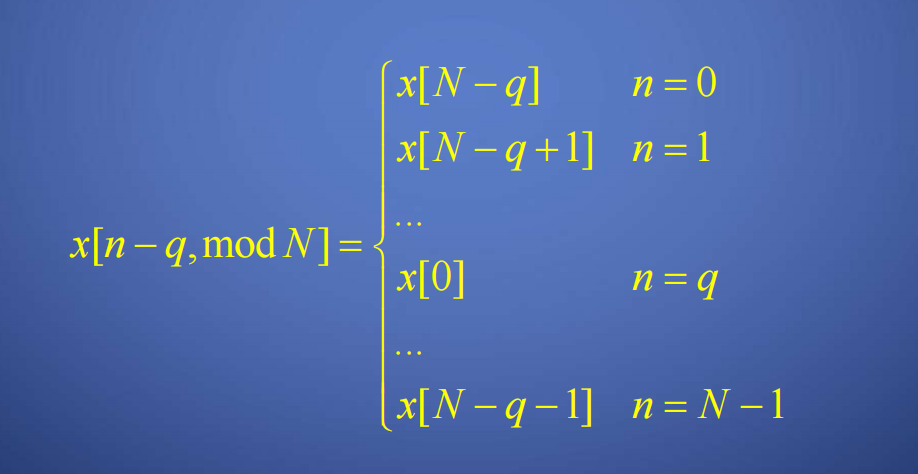
循环反褶的定义同理

圆周频移
圆周卷积
前提条件:N一致且有限长
符号用\(\circledast\)表示 $$ x_1[n]\circledast x_2[n]=\sum_{k=0}^{N-1}x_1[k]x_2[n-k, \text{mod } N] $$
圆周卷积长度为N $$ x[n]\circledast \delta[n-n_0]=x[n-n_0,\text{mod }N] $$
3.圆周卷积与线性卷积

圆周卷积可以用计算机来处理,而线性卷积无法使用计算机来处理,因此我们可以使用圆周卷积来计算线性卷积。
具体做法为通过补零将需要卷积的信号拓展为\(2N-1\)的序列,此时线性卷积=圆周卷积
用\(y_L[n]\)表示线性卷积结果,\(y_C[n]\)表示圆周卷积结果
当\(N=L_1+L_2-1\)时,\(y_L[n]=y_C[n]=\text{IDFT}(Y_k)\)
当\(N>L_1+L_2-1\)时,\(y_L[n]=y_C[n]R_N[n]=\text{IDFT}(Y_k)R_N[n]\)
4.基于 DTFT 和 DFT 的系统分析
LTI 系统的频域DTFT分析
对于一个没有初始能量的系统,输入 \(x[n]\) 对应的输出响应 \(y[n]\) 由卷积和给出: $$ y[n] = h[n] * x[n] = \sum_{i=-\infty}^{\infty} h[i]x[n-i] $$ 如果单位脉冲响应 \(h[n]\) 是绝对可和的(即系统稳定): $$ \sum_{n=-\infty}^{\infty} |h[n]| < \infty $$ 则系统的频率响应函数(Frequency response function)定义为 \(h[n]\) 的 DTFT: $$ H(\Omega) = \sum_{n=-\infty}^{\infty} h[n]e^{-j\Omega n} $$ 此时,时域的卷积对应频域的乘积: $$ Y(\Omega) = H(\Omega)X(\Omega) $$
幅频特性与相频特性
系统的输出频谱 \(Y(\Omega)\) 可以分解为幅度和相位两部分:
幅频特性(Magnitude function) $$ |Y(\Omega)| = |H(\Omega)| \cdot |X(\Omega)| $$ 即输出的幅度谱等于系统频率响应的幅度谱与输入信号幅度谱的乘积。
相频特性(Phase function) $$ \angle Y(\Omega) = \angle H(\Omega) + \angle X(\Omega) $$ 即输出的相位谱等于系统频率响应的相位谱与输入信号相位谱之和。
输入为正弦序列的系统响应
当 LTI 系统的输入为正弦/余弦序列时: $$ x[n] = A \cos(\Omega_0 n + \theta), \quad n = 0, \pm 1, ... $$ 该输入信号的 DTFT 为: $$ X(\Omega) = \sum_{k=-\infty}^{\infty} A\pi [e^{-j\theta}\delta(\Omega + \Omega_0 - 2\pi k) + e^{j\theta}\delta(\Omega - \Omega_0 - 2\pi k)] $$ 经过频率响应为 \(H(\Omega)\) 的系统后,输出响应 \(y[n]\) 为: $$ y[n] = A |H(\Omega_0)| \cos(\Omega_0 n + \theta + \angle H(\Omega_0)) $$
LTI 系统的频域DFT分析
需要解决的问题是已知\(X_k,H_k\),求\(y[n]\)
\(y[n]=x[n]*h[n],X_kH_k\leftrightarrow x[n]\circledast h[n]\),此时,需要圆周卷积=线性卷积
5.FFT(Fast Fourier Transform)
FFT 并不是一种新的变换,而是 DFT 的一种高效算法。这里介绍的是按时间抽取的基2-FFT算法 (Decimation-in-Time, DIT-FFT)。
DFT运算数量级
\(N^2\)次复数乘法,\(N(N-1)\)复数加法,\(N\)较大时运算复杂度较高
算法思路与分组
设序列 \(x[n]\) 的长度为 \(N\),且满足 \(N=2^L\)(即 \(N\) 为 2 的整数次幂)。
将序列 \(x[n]\) 按 \(n\) 的奇偶性分为两组,每组长度为 \(N/2\): $$ a[n] = x[2n] $$
子序列的 DFT
分别对偶数序列 \(a[n]\) 和奇数序列 \(b[n]\) 进行 \(N/2\) 点的 DFT: $$ A_k = \text{DFT}(a[n]) = \sum_{n=0}^{N/2-1} a[n]W_{N/2}^{kn} $$
其中 \(k = 0, 1, ..., \frac{N}{2}-1\)。
推导过程
利用旋转因子 \(W_N\) 的性质:
- 可约性:\(W_N^{2n} = W_{N/2}^n\)
- 周期性:\(A_k\) 和 \(B_k\) 的周期均为 \(N/2\),即 \(A_{k+N/2} = A_k\)
- 对称性:\(W_N^{k+N/2} = -W_N^k\)
原信号 \(x[n]\) 的 \(N\) 点 DFT 可以表示为: $$ X_k = \sum_{n=0}^{N-1} x[n]W_N^{kn} $$ 将其拆分为偶数项和奇数项的和: $$ X_k = \sum_{n=0}^{N/2-1} x[2n]W_N^{k(2n)} + \sum_{n=0}^{N/2-1} x[2n+1]W_N^{k(2n+1)} $$
由此得到前一半区间 (\(0 \le k < N/2\)) 的公式: $$ X_k = A_k + W_N^k B_k $$
完整 FFT 算法 (蝶形运算)
由于 \(A_k\) 和 \(B_k\) 只有 \(N/2\) 个点,对于后一半区间 (\(N/2 \le k < N\)),我们需要利用对称性求解。
令 \(k' = k + N/2\),其中 \(k\) 的范围仍为 \(0\) 到 \(N/2-1\)。 $$ X_{k+N/2} = \sum_{n=0}^{N/2-1} a[n]W_{N/2}^{(k+N/2)n} + W_N^{k+N/2} \sum_{n=0}^{N/2-1} b[n]W_{N/2}^{(k+N/2)n} $$ 利用 和 \(W_N^{k+N/2} = -W_N^k\),可得: $$ X_{k+N/2} = A_k - W_N^k B_k $$ 综上所述,完整的 FFT 蝶形运算公式为:
对于 \(k = 0, 1, ..., \frac{N}{2}-1\): $$ X_k = A_k + W_N^k B_k $$
通过这种方式,将一个 \(N\) 点的 DFT 分解为两个 \(N/2\) 点的 DFT,并通过加减运算(蝶形运算)组合,运算量降低至\(\frac{N^2+N}{2}\)。
计算完\(N/2\)后,可以继续往下计算,整体思路如下图。
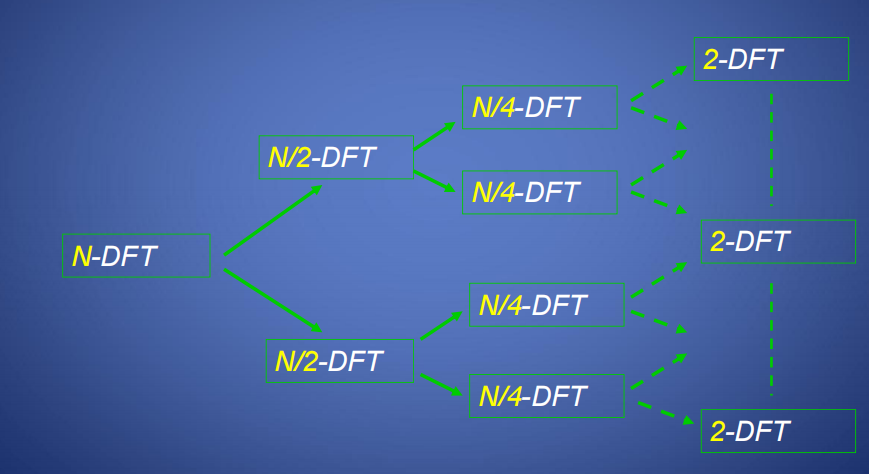
以8点为例
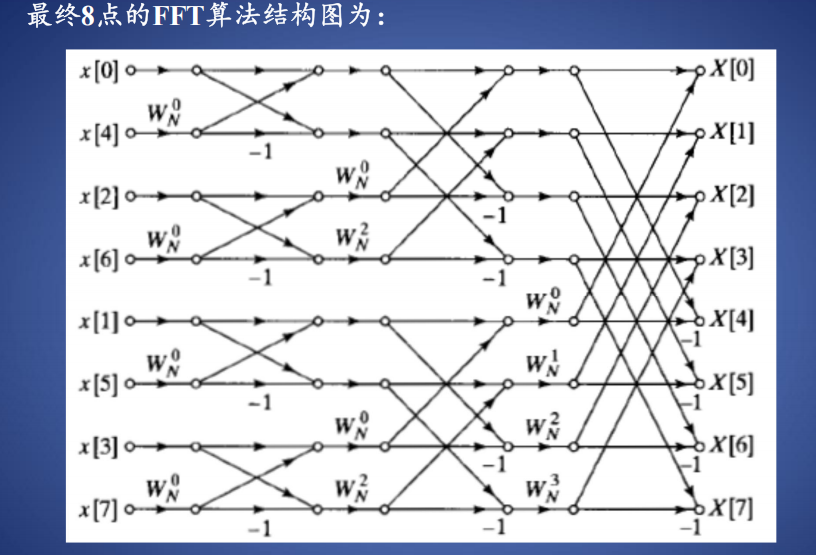
每个蝶形运算:1次复数乘法,2次复数加法
整个FFT运算复杂度:\((N/2)\log_2 N\) 个蝶形运算
排序最小单元
二进制数列倒序,如\(001\rightarrow 100\)
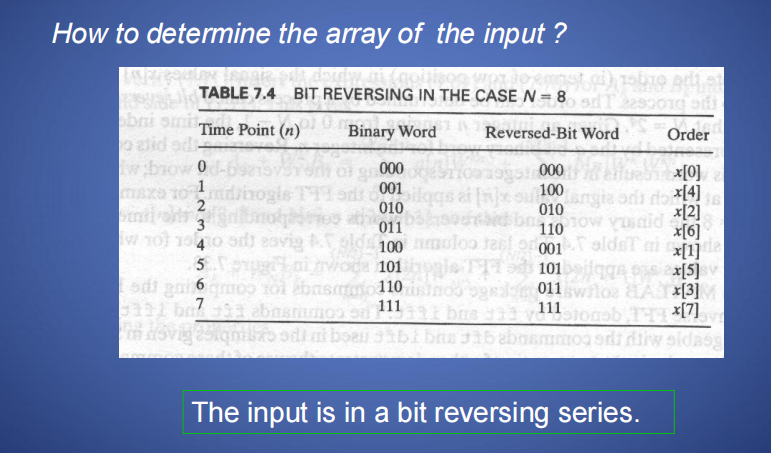
理解

6.傅里叶变换总结回顾
连续周期信号傅里叶级数
连续周期信号的傅里叶变换后的信号是离散,非周期的
连续非周期信号的傅里叶变换
连续非周期信号傅里叶变换后的信号是连续
DTFT
离散非周期时间信号的傅里叶变换\(X(\Omega)\)是周期、连续的
离散周期时间信号的傅里叶变换\(X(\Omega)\)是周期、离散的,如\(\cos(\Omega_0 n)\)
DFT
DFT是对DTFT的采样,是离散的